Answers
Answer:
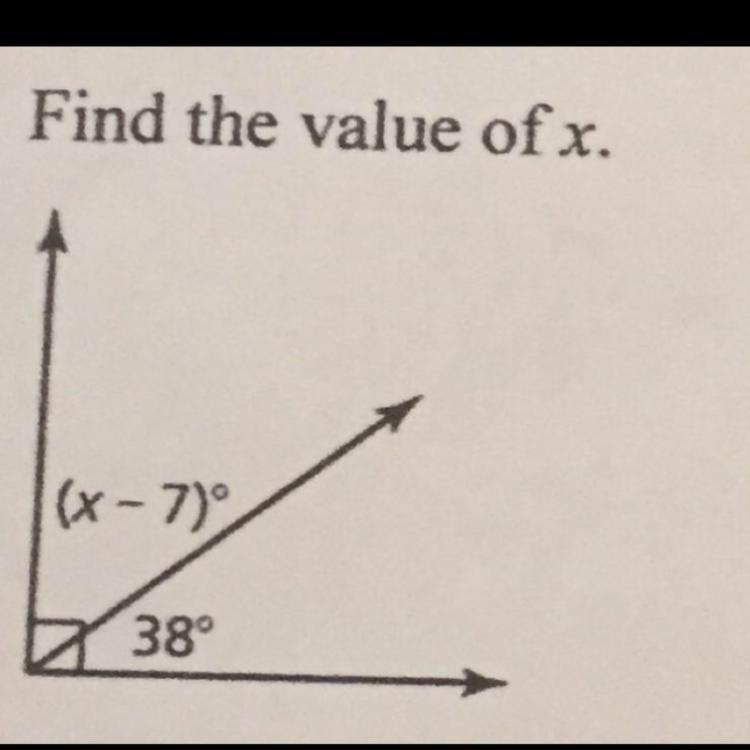
x = 59°
Step-by-step explanation:
The square symbol shown in the angle means that it is 90°. We can say that the angle x - 7 and 38 add up to 90 because of that. We can set up an equation to model the situation:
x - 7 + 38 = 90
x + 31 = 90
x = 59°
Related Questions
Which fraction is equivalent to 1/6
1/3
2/8
3/24
4/24
Answers
Answer:
the last one- 4/24
Step-by-step explanation:
ive answered this question before and got it correct
Simplify the expression using order of operation 5 x 2 + 3 to the power of 2
Answers
answer= 1
5 x 2 - 3^2
1. First simplify exponents
= that is nine
2. Then Do 5 x 2- 9
5 x 2=10
10-9
= 1
Benny has two small fish tanks with one fish in each tank. One tank has 3 1/2 quarts of water. The other tank has 6 pints of water. Benny combines the water into one large fish tank with both fish in the large tank. How many pints of water are in the large tank?
Answers
Answer:
6 1/2 quarts I think
Step-by-step explanation:
So sorry if I'm wrong! Have a nice day! Owa Owa!
A filtration process removes a random proportion of particulates in water to which it is applied. Suppose that a sample of water is subjected to this process twice. Let x1 be the proportion of the particulates that are removed by the first pass. Let X2 be the proportion of what remains after the first pass that is removed by the second pass. Assume that X1 and X2 are independent random variables with common pdf. f(x) = 4x3, for 0 < x <1 and f(x) = 0 otherwise. Let Y be the proportion of the original particulates that remain in the sample after two passes. Then Y = (1 - X1)(1 - X2). Find E(Y).
Answers
Answer:
[tex]E(Y)=\frac{1}{25}[/tex]
Step-by-step explanation:
Let's start defining the random variables for this exercise :
[tex]X_{1}:[/tex] '' The proportion of the particulates that are removed by the first pass ''
[tex]X_{2}:[/tex] '' The proportion of what remains after the first pass that is removed by the second pass ''
[tex]Y:[/tex] '' The proportion of the original particulates that remain in the sample after two passes ''
We know the relation between the random variables :
[tex]Y=(1-X_{1})(1-X_{2})[/tex]
We also assume that [tex]X_{1}[/tex] and [tex]X_{2}[/tex] are independent random variables with common pdf.
The probability density function for both variables is [tex]f(x)=4x^{3}[/tex] for [tex]0<x<1[/tex] and [tex]f(x)=0[/tex] otherwise.
The first step to solve this exercise is to find the expected value for [tex]X_{1}[/tex] and [tex]X_{2}[/tex].
Because the variables have the same pdf we write :
[tex]E(X_{1})= E(X_{2})=E(X)[/tex]
Using the pdf to calculate the expected value we write :
[tex]E(X)=\int\limits^a_b {xf(x)} \, dx[/tex]
Where [tex]a=[/tex] ∞ and [tex]b=[/tex] - ∞ (because we integrate in the whole range of the random variable). In this case, we will integrate between [tex]0[/tex] and [tex]1[/tex] ⇒
Using the pdf we calculate the expected value :
[tex]E(X)=\int\limits^1_0 {x4x^{3}} \, dx=\int\limits^1_0 {4x^{4}} \, dx=\frac{4}{5}[/tex]
⇒ [tex]E(X)=E(X_{1})=E(X_{2})=\frac{4}{5}[/tex]
Now we need to use some expected value properties in the expression of [tex]Y[/tex] ⇒
[tex]Y=(1-X_{1})(1-X_{2})[/tex] ⇒
[tex]Y=1-X_{2}-X_{1}+X_{1}X_{2}[/tex]
Applying the expected value properties (linearity and expected value of a constant) ⇒
[tex]E(Y)=E(1)-E(X_{2})-E(X_{1})+E(X_{1}X_{2})[/tex]
Using that [tex]X_{1}[/tex] and [tex]X_{2}[/tex] have the same expected value [tex]E(X)[/tex] and given that [tex]X_{1}[/tex] and [tex]X_{2}[/tex] are independent random variables we can write [tex]E(X_{1}X_{2})=E(X_{1})E(X_{2})[/tex] ⇒
[tex]E(Y)=E(1)-E(X)-E(X)+E(X_{1})E(X_{2})[/tex] ⇒
[tex]E(Y)=E(1)-2E(X)+[E(X)]^{2}[/tex]
Using the value of [tex]E(X)[/tex] calculated :
[tex]E(Y)=1-2(\frac{4}{5})+(\frac{4}{5})^{2}=\frac{1}{25}[/tex]
[tex]E(Y)=\frac{1}{25}[/tex]
We find that the expected value of the variable [tex]Y[/tex] is [tex]E(Y)=\frac{1}{25}[/tex]
Pls answer this. I need the answer quick. Just write the answer. no downloads
Answers
Answer:
POINTS HA
Step-by-step explanation:
I need helppppppppppp
Answers
Answer:
b.)36
Step-by-step explanation:
Formula for area of a trapezoid = [tex]\frac{a+b}{2} h[/tex]
where a and b = bases and h = height
The sign has the following dimensions
Base 1 = 6ft
base 2 = 12ft
height = 4ft
Using these dimensions we plug in the values into the formula
[tex]A=\frac{6+12}{2} 4\\6+12=18\\\frac{18}{2} =9\\9*4=36[/tex]
Hence the area of Mr. Wash's sign is 36 square feet.
Answer:
b) 36 sq ft.
Step-by-step explanation:
6 x 4 = 24 (multiply to find the square after splitting it)
12 - 6 = 6 x 4 = 24 / 2 = 12 (you divide by two because it's a triangle)
24 + 12 = 36
hope this helps :)
What is the solution to the equation below round your answer to two decimal decimal places log4 x=2.1
A. x=8.40
B. x=18.38
C. x=8.17
D. x=19.45
Answers
Answer:
B 18.38
Step-by-step explanation:
log4x = 2.1
logx/log4 = 2.1
logx = log(4) x 2.1
logx = 1.2643
x = antilog(1.2643)
x = 18.38 (to 2 d.p)
Answer:
X=18.38
Step-by-step explanation:
Convert x=-3 to polar equation
Answers
(
x
,
y
)
is written as
(
r
,
θ
)
in polar coordinates, then
x
=
r
o
s
θ
and
y
=
r
sin
θ
.
As such in polar form equation
x
=
−
3
can be written as
r
cos
θ
=
−
3
or
r
=
−
3
cos
θ
A complex electronic system is built with a certain number of backup components in its subsystems. One subsystem has eight identical components, each with a probability of 0.1 of failing in less than 1,000 hours. The sub system will operate if any four of the eight components are operating. Assume that the components operate independently. Find the probability that
a. exactly two of the four components last longer than 1000 hours.
b. the subsystem operates longer than 1000 hours.
Answers
Answer:
a) 0.0486 = 4.86% probability that exactly two of the four components last longer than 1000 hours.
b) 0.9996 = 99.96% probability that the subsystem operates longer than 1000 hours.
Step-by-step explanation:
For each component, there are only two possible outcomes. Either they last more than 1,000 hours, or they do not. Components operate independently, which means that the binomial probability distribution is used to solve this question.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.
[tex]P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}[/tex]
In which [tex]C_{n,x}[/tex] is the number of different combinations of x objects from a set of n elements, given by the following formula.
[tex]C_{n,x} = \frac{n!}{x!(n-x)!}[/tex]
And p is the probability of X happening.
One subsystem has eight identical components, each with a probability of 0.1 of failing in less than 1,000 hours.
So 1 - 0.1 = 0.9 probability of working for more, which means that [tex]p = 0.9[/tex]
a. exactly two of the four components last longer than 1000 hours.
This is P(X = 2) when [tex]n = 4[/tex]. So
[tex]P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}[/tex]
[tex]P(X = 2) = C_{4,2}.(0.9)^{2}.(0.1)^{2} = 0.0486[/tex]
0.0486 = 4.86% probability that exactly two of the four components last longer than 1000 hours.
b. the subsystem operates longer than 1000 hours.
The subsystem has 8 components, which means that [tex]n = 8[/tex]
It will operate if at least 4 components are working correctly, so we want:
[tex]P(X \geq 4) = 1 - P(X < 4)[/tex]
In which
[tex]P(X < 4) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)[/tex]
So
[tex]P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}[/tex]
[tex]P(X = 0) = C_{8,0}.(0.9)^{0}.(0.1)^{8} \approx 0[/tex]
[tex]P(X = 1) = C_{8,1}.(0.9)^{1}.(0.1)^{7} \approx 0tex]
[tex]P(X = 2) = C_{8,2}.(0.9)^{2}.(0.1)^{6} \approx 0[/tex]
[tex]P(X = 3) = C_{8,3}.(0.9)^{3}.(0.1)^{5} = 0.0004[/tex]
Then
[tex]P(X < 4) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) = 0 + 0 + 0 + 0.0004 = 0.0004[/tex]
[tex]P(X \geq 4) = 1 - P(X < 4) = 1 - 0.0004 = 0.9996[/tex]
0.9996 = 99.96% probability that the subsystem operates longer than 1000 hours.
find lim h->0 f(9+h)-f(9)/h if f(x)=x^4 a. 23 b. -2916 c. 2916 d. 2925
Answers
[tex]\displaystyle\lim_{h\to0}\frac{f(9+h)-f(9)}h = \lim_{h\to0}\frac{(9+h)^4-9^4}h[/tex]
Carry out the binomial expansion in the numerator:
[tex](9+h)^4 = 9^4+4\times9^3h+6\times9^2h^2+4\times9h^3+h^4[/tex]
Then the 9⁴ terms cancel each other, so in the limit we have
[tex]\displaystyle \lim_{h\to0}\frac{4\times9^3h+6\times9^2h^2+4\times9h^3+h^4}h[/tex]
Since h is approaching 0, that means h ≠ 0, so we can cancel the common factor of h in both numerator and denominator:
[tex]\displaystyle \lim_{h\to0}(4\times9^3+6\times9^2h+4\times9h^2+h^3)[/tex]
Then when h converges to 0, each remaining term containing h goes to 0, leaving you with
[tex]\displaystyle\lim_{h\to0}\frac{f(9+h)-f(9)}h = 4\times9^3 = \boxed{2916}[/tex]
or choice C.
Alternatively, you can recognize the given limit as the derivative of f(x) at x = 9:
[tex]f'(x) = \displaystyle\lim_{h\to0}\frac{f(x+h)-f(x)}h \implies f'(9) = \lim_{h\to0}\frac{f(9+h)-f(9)}h[/tex]
We have f(x) = x ⁴, so f '(x) = 4x ³, and evaluating this at x = 9 gives the same result, 2916.
A rectangle is graphed on a coordinate plane. The rectangle’s two lines of symmetry are the x-axis and the y-axis. Evie says that means the vertices are reflections of each other over the x-axis and y-axis. Is she correct? Explain your reasoning NO LINKS worth 50 points
Answers
Answer:
Can you add a picture if there are any?
Step-by-step explanation:
What is the volume please help me
Answers
Answer:
125 inches cubed
Step-by-step explanation:
First, you find the volume of the full square, and then you divide your answer by 2, since the figure is a triangle.
So,
10 x 10 x 2.5 = 250
250 ÷ 2 = 125 inches cubed
What is the zero of function f?
f(x)=7^3Vx+12-12
Answers
Answer:
hope it helps ya.
please give me brainliest
$500.00 at 4% for 5 years
50 points if you anwser asap
Answers
Answer:
100
Step-by-step explanation:
it gives you the formula for simple interest
What is the probability of a coin landing on heads 3 times?
Answers
Answer:
50%
Step-by-step explanation:
Suppose you have a fair coin; this means it has a 50% chance of landing heads up. Suppose you dip it three times, these flips are independent. What is the probability that it lands heads up, then tails up and then heads up again. so the answer is 1/8 or 12.5%
(hope I wasnt late!!)
Help look at picture no links!!!
Answers
Answer:
B
Step-by-step explanation:
Angle 1 is an exterior angle, while angle 6 is an interior angle and so they are not congruent
Find the indicated values. Geometry.
Answers
Answer:
1. x=16
2. x=35
3. x=10
4. x=30
5. x=3
Step-by-step explanation:
intercepted arcs are 2* the angle measure
1. x= 1/2( 32)=16 x=16
2. the intercepted arc is 360-110-180=70
1/2(70)= 35
3. 2x=x+10 subtract x from both sides
x=10
4. 2(x+30)=4x
2x+60=4x
60=2x
30=x
5. 2(3x)=12x-18
6x=12x-18
-6x=-18
x=m
what's the standard equation of the circle with the general equation x2 + y2 + 4x - 2y - 20 = 0
Answers
Answer:
(x+2)2+(y-1)2=25
Step-by-step explanation:
x2+y2+4x-2y+4+1=20+4+1
How many 5-digit numbers can be formed if each one uses all the digits 0,1,2,3,4
without repetition?
Answers
Answer:
{0, 1, 2, 3, 4} --> 96 5-digit numbers possible with this set.
Step-by-step explanation:
i dunno, i kinda just searched it up
link: https://gmatclub.com/forum/how-many-five-digit-numbers-can-be-formed-using-digits-91597.html#:~:text=If%200%20is%20included%3A,numbers%20possible%20with%20this%20set.
Answer:
120
Step-by-step explanation:
using the equation 5P5, you find that the total number of ways these 5 digits can be arranged to form 5 digit numbers if each is only used ONCE.
please help this is very important i will give you brain thing if its correct and no links pwease <3
Answers
Answer:
the 2nd and 3rd one I believe
You go to the doctor and he gives you 11 milligrams of radioactive dye. After 12 minutes, 7.75 milligrams of dye remain in your system. To leave the doctor's office, you must pass through a radiation detector without sounding the alarm. If the detector will sound the alarm if more than 2 milligrams of the dye are in your system, how long will your visit to the doctor take, assuming you were given the dye as soon as you arrived
Answers
Answer:
In (16.8+12=) 28.8 minutes the person will be left only with 2mg of dye in the body and be able to leave the doctor's office after being injected with 11 mg
Step-by-step explanation:
After 12 minutes, 7.75 milligrams of dye remain in your system.
This means that 11- 7.75= 3.25 milligrams of dye are used up in 12 minutes
7.75-2= 5.75 milligrams still needs to be used up
Dye Minutes
3.25 12
5.75 x
x= 12*5.75/3.25
x= 16.8 minutes
5.75 mg will be used up in 16.8 minutes
In (16.8+12=) 28.8 minutes the person will be left only with 2mg of dye in the body and be able to leave the doctor's office.
A very weak university is on and off probationary status with the accrediting agency. A different procedure is used in July and in January to determine its status for the next 6 months. In July, the probability of changing status by coming off probation is .25; but the probability of changing status by going on probation is .12. In January, the probability of coming off probation is .15; but the probability of going on probation is .08. a) If the university is on probation as of February 2019; what is the probability it will be off probation in February 2020
Answers
Answer:
0.3425 = 34.25% probability it will be off probation in February 2020
Step-by-step explanation:
We have these desired outcomes:
Off probation in July 2019, with 0.25 probability, then continuing off in January, with 1 - 0.08 = 0.92 probability.
Still in probation in July 2019, with 1 - 0.25 = 0.75 probability, then coming off in January, with 0.15 probability.
What is the probability it will be off probation in February 2020?
[tex]p = 0.25*0.92 + 0.75*0.15 = 0.3425[/tex]
0.3425 = 34.25% probability it will be off probation in February 2020
Is 6.584 a rational number
Answers
What's your numerator and denominator value?
What is the volume (in cubic units) of a cylinder with a radius of 3 units and a height of 12 units?
Answers
If a =5 and b=3 what is the value of the 2a-3b+3a
Answers
Answer:
If a = 5 and b = 3, then that means 2a - 3b + 3a = 16
Step-by-step explanation:
2a - 3b + 3a
(2×5) - (3×3) + (3×5)
10 - 9 + 15 = 16
No random links or answers, please.
Answers
Answer:
the ans is 21 hope it may help u
Step-by-step explanation:
g = 6
x=6
x= 3x + 3
x = 3 × 6 +3
x = 18 + 3
x= 21
Leroy wants to teach his puppy 6 new tricks. In how many different orders can the puppy learn the tricks?
Answers
Answer: 720 ways
Step-by-step explanation:
Given
Leroy wants to teach his puppy 6 new tricks
Considering each trick is different from other
The first trick can be taught in 6 different ways
After learning the first trick, there are 5 tricks remaining which can be taught in 5 different ways
Similarly, for the remaining tricks, it is 4, 3, 2, and 1 way
So, the total number of ways is [tex]6\times 5\times 4\times 3\times 2\times 1=720\ \text{Ways}[/tex]
Find the median of each set of data
Answers
Answer:
sorry, I think u got yr question incomplete.
stay safe healthy and happy.To find the median:
- Arrange the data points from smallest to largest.
- If the number of data points is odd, the median is the middle data point in the list.
- If the number of data points is even, the median is the average of the two middle data points in the list.
what is 8/3x-x+5/3=13/6-2/3x
Answers
Answer:
Step-by-step explanation:
What is the completely factored form of f(x)=x3+4x2+9x+36 ?
f(x)=(x+4)(x−3)(x+3)
f(x)=(x−4)(x−3i)(x+3i)
f(x)=(x+4)(x−3i)(x+3i)
f(x)=(x−4)(x−3)(x+3)
Answers
Hereaaaaaaaaaaaaaaaaaaaaaaaaaaa